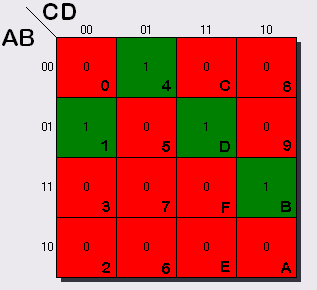
|
As stated in the manual, 8 wires control each of the 8 different LED positions on all 7-segment displays. Therefore, only a single decoder unit is required to control all four sections of the display. We wish to create a Verilog module that converts a 4-bit number into a hexadecimal representation, hence we must first find out the relationship between each of the bits of the 7-segment display and the decimal representation of the binary numbers. For instance, the top most middle bit (called CA in the manual) will only light up for the hexadecimal numbers: 0, 2, 3, 5, 6, 7, 8, 9, A, C, E, F.
This is where our the Karnaugh maps technique that you learnt in last year's digital circuits course comes into play. Each element of the 7-segment display is controlled by its relationship to the binary representation of the hexadecimal number, which is 4-bits wide. Hence it is possible to use a Karnaugh map to derive the Boolean expression that will correctly determine if an element should be on or off for each of the hexadecimal numbers. To get back to our example of element CA, the Karnaugh map looks like the following if A, B, C, and D are the bits of the 4-bit binary number (CDBA):
This can be coded in Boolean by using the following syntax:
'~' = Boolean not
'&' = Boolean and
'|' = Boolean or
'^' = Boolean xor though you do not need to use this here
Therefore the skeleton of the entire module with only the first bit coded would look like the following.
The 'assign' statements are used to simplify the Boolean expressions, separating each of the incoming bits, defining them as A, B, C and D. Now all you need to do is draw the Karnaugh maps, and derive the Boolean expression for the other 6 LED sections.
Note that, in reality, deriving the minimal sum of products expressions is not necessary as the synthesis tool has a logic reduction functionalty which will map any boolean function efficiently on to FPGA hardware. Hence, nowadays, hardware designers do not usually spend much time reducing logic expressions but instead express the boolean functions in the most convenient way to them, knowing that synthesis tools are now capable of automatically deriving the most efficient mappings to silicon.
|